A change in topic... to trees

Yeah, yeah, I know. I've basically abandoned this blog after my kid was born. Well, I'm back. I may continue working on the toast problem, but in the mean time, here are some random thoughts I had a little while ago.

I was on an elliptical machine recently, bored out of my mind because nothing good was on TV. (This experience only reinforced my desire to exercise only outside, and never to watch TV.) I was staring out the window, I looked straight into a medium sized tree. I decided to use this tree to entertain me, and since I’m not one for poetry, I decided to calculate how many leaves were on it. Calculate, not count. I wasn’t going to count them, because 1. I don’t know how I could keep count of such a thing, and 2. I wasn’t that bored. Instead, I was going to calculate it.

Here’s what I decided to do. First, I’d imagine a model for how the leaves are distributed. Then, I’d use that model to calculate how many leaves are on the tree. Looking the tree, it occurred to me that most of the leaves are on the outer-most branches. When you climb a tree, you scramble up the thickest branches and don’t have much trouble with leaves where you want to put your hands and feet. This makes sense, the leaves grow on the outermost branches in the sun, and they shade the thick trunk and main branches near the center. Therefore, the center branches don’t get much sun direct sunlight and have no need for leaves. There’s probably a name for this organization, but I haven’t studied enough biology to know what it is called.

First, I calculated the surface area of the tree. My tree was tall and somewhat skinny. I estimated it had a diameter (d) of about 3 meters (about 10 feet) and height (h) of 6 meters (about 20 feet). I approximated this as the outer surface of a cylinder, with an area of πdh. (πd is the circumference of a circle, often written 2πr, where the radius is half the diameter, so 2r=d.) Using my numbers above, I got about 54 m2 area.

Each leaf was about 2 cm by 3 cm, for an area of 6 cm2, or 0.0006 m2. (Notice that 1 m2 = 10,000 cm2, even though 1 m = 100 cm. This is something I remember getting wrong in high school. 1m times 1 m is 1 m2, but this is the same thing as 100 cm (= 1 m) times 100 cm = 10,000 cm2.) Therefore, if the outer surface was covered with a single layer of leaves, it would take 54 m2 / 0.0006 m2 / leaf = 90,000 leaves to cover it.

Looking at the center of the tree from where I was standing, it seemed like there were two or three leaves blocking my view of the center of the tree. It makes sense that there are more than one, because if that one leaf were to get eaten by insects, the tree would miss out on the sun shining in that area. However, there isn’t any need for 50 leaves in one area, because that would be too many extra leaves in that one spot. The probability of 49 leaves getting eaten and only one being left behind is too low to make 50 leaves per location necessary. The true number is probably somewhere between 1 and 10, so I multiply my “single layer” value of 90,000 leaves by 3, and get an estimate of 270,000 leaves.

A small tree with big leaves might have considerably less than this – maybe only 30,000 leaves. Meanwhile a big tree with small leaves could probably have millions of leaves. There are some types of trees that are HUGE and grow tiny leaves, the weeping willow is one, and perhaps they grow tens of millions (maybe a hundred?) million leaves. Next time I see a weeping willow, I can make some measurements and calculate.

OK, so was I right? I don't have any books about tree biology, and I don't know if they would contain such trivial info if I did. So, I turned to the lazy person's answer book: the internet! Answers I found ranged from unsupported but purportedly authoritative statements of "an oak tree has about 200,000 leaves" , to estimates based on ground coverage. Both of these agree with my estimate, but I'd like a more biologically derived response. How many leaves should a tree grow. I tried using google scholar and found that there are too many other uses for tree (information theory, computer science...) and couldn't find any biology papers. I guess verification of my model has left me stumped, no pun intended.

5. A Simple View of Tumbling Toast

As previously discussed, Toast is likely to fall after being perched on the edge of a Table, Counter, or Clumsy Hand. Starting from this initial condition, the Toast topples off the Ledge and then falls to the Floor. In my last post, I found that the Buttered Side Down condition is determined by four parameters describing the Toast’s motion when it leaves contact with the Table. These parameters are the initial velocity component in the vertical direction (v_v), the height above the Floor (h₀), the angle relative to the Buttered Side Up starting position of the Toast (θ₀), and the rotation rate (ω). For quick browsing, I’ll highlight a section in red when I determine the value of a parameter.

(Before scaring readers away, I’ll warn you that the math in the following sections makes it easier (NOT HARDER) to understand what’s going on. An equation is worth a thousand words, or something like that. The math will be nothing more than 9th grade algebraic substitution and rearrangement. Equations will also be followed by a colored section in parenthesis that briefly discusses its meaning and can be skipped if considered obvious.)

What follows is a simple calculation based on some pretty coarse approximations, which may be relaxed in future calculations. However, these simple approximations will provide quite a bit of insight about rigid pieces of Toast as they topple. The initial condition is drawn in Figure 5.1a, representing 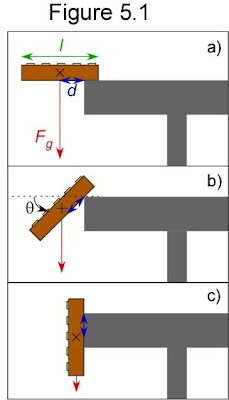Toast positioned with its center of mass (marked with an x) overhanging a Table Ledge by a small distance d. As discussed at length previously, the force of gravity will cause the Toast to rotate, slip, and fall from the Ledge.

My first approximation is that the Toast cannot slide while on the Table Ledge. Thus, rotation occurs as drawn in Figure 5.1b with the Toast rotating around the line of contact between its bottom surface and the Table until the Toast is vertical (θ = 90°, Figure 5.1c), at which point it falls. Using this approximation, I have already constrained one of my parameters; θ₀ must be 90° when the free fall starts.

In Figure 5.1a, the Toast overhangs the Ledge by a distance d. Because there is no sliding, the Toast’s center of mass has been lowered by d when it reaches the position in Figure 5.1c. Since d is much smaller than the length of the Toast (l), approximately all the gravitational energy (E_g) released by lowering the Toast’s center of mass by d is deposited in the Toast’s rotation (call this E_rot). Mathematically,

(5.1a) E_rot ≅ -E_g
(5.1b) = m g d

(Here, m is the mass of the Toast, and g is the acceleration due to gravity. The energy released in lowering the Toast increases with d, m, and the “strength” of gravity, g. Therefore, it makes sense that these three values are multiplied together in Equation 5.1. Don't worry too much about the negative sign; it just makes sure that decreasing E_g, as the Toast is lowered, becomes increasing E_rot, as it spins faster.)

I use an approximately equal sign (≅) in Equation 5.1 because as the Toast topples (on the Ledge), rotation occurs along the line of contact between the Toast and the Ledge. Once it enters free fall, rotation occurs around an axis through the center of mass. Since the displacement between these two axes is small (≅d), I have ignored the detailed transformation between them and assumed all the energy becomes rotation about the proper freely rotating axis. This is another approximation to be addressed in detail another time.

It turns out that this approximation immediately determines another of my parameters. Since all the energy goes into rotation, none can be in translation and v_v must be zero. Another parameter can be constrained using a little bit of math because E_rot determines the speed of rotation (also called the angular velocity, ω) according to

(5.2) E_rot = ¹/₂ I ω² .

(I is the moment of inertia, which increases as the Toast becomes heavier or larger, and therefore harder to spin. It plays a similar role as mass does in linear [non rotating] motion, where the energy E_linear = ¹/₂ m v² is isomorphic with Equation 5.2.)

By substituting the expression on the right side of Equation 5.1 in Equation 5.2 and solving for ω, we find the expression for the Toast’s angular velocity as it leaves the Table:

(5.3) ω = √(2m g d / I).

(It is helpful to have a physical picture for an equation. For Equation 5.3, it helps if you are familiar with how a quantity scales with the square root of a variable. Plotting a graph of the square root of x versus x can help. That is how ω increases with d and 1/I, i.e. it doubles when they go up by four, triples when they increase by nine, and so on. More importantly, Equation 5.3 reveals that the Toast’s rotation (ω) increases as we increase the terms related to the gravitational energy: m, g, and d. On the other hand, it decreases as I gets bigger because I is dividing the other terms. Such a decrease makes sense because bigger I means it is harder to spin the Toast.)

Now all we need to know is how far the Toast falls, h₀. One likely height is that of a Table or countertop. A very low Table, such as a Coffee Table, is probably the lowest the Toast is likely to fall from. (Perhaps you sometimes put food on the Floor, in which case, no, I won't join you for dinner.) An upper limit of the initial height might be the height of a clumsy person’s mouth while standing. In this model, h₀ is actually these heights MINUS d. However, d is very small and h₀ is not very well defined, so I will ignore this very minor correction. In fact, I’ll keep h₀ as a variable, so we can see how the results change as it is varied over the range just defined.

(On that note, I’m also neglecting another term: the change in h₀ caused by the angle of the Toast bringing its edge in contact with the Floor before the center of mass. That is, when the Toast is parallel to the Floor (θ = 0° or 180° as in Figure 5.1a) when it lands, the entire Toast has fallen by h₀. However, when the Toast has rotated 90° (as in Figure 5.1c), the edge that hits first has fallen h₀ MINUS l/2, because that edge of the Toast is l/2 closer to the Floor when θ = 90°. Again, l/2 is much smaller than h₀, so I’ll ignore this for now and include it explicitly later.)

HOW MUCH DOES THE TOAST ROTATE BEFORE HITTING THE GROUND?

We answer this question by substituting t = t_f via Equation 4.3 ( t_f = √ ( 2 h₀)and Equation 4.4 (θ(t) = θ₀ + ω t) from my last post, and then expressing ω according to Equation 5.3, above, to find

(5.4a) θ = θ₀ + √(2m g d / I) √ ( 2 h₀ / g)
(5.4b) = θ₀ + 2 √(m d h₀ / I) .

This tells us how far the Toast rotates after falling a distance h₀. Before getting into the “numbers” of the result, we can learn more about the situation by examining how Equation 5.4 scales with various quantities. θ increases with the height of the fall, h₀, and the amount the Toast initially hangs over the Ledge, d. Although there seems to be some mass dependence, this actually cancels because I is proportional to m, and the ratio of the two is a term that only depends on the shape of the Toast and other geometric factors to be worked out in detail some other time.

More important is what Equation 5.4 does NOT depend upon. Notice that there is NO dependence on g, the acceleration due to gravity. What does this mean? Well, g has a particular value on the surface of Earth, another one on the moon, and another one in an accelerating spaceship. It could take almost any value depending on where you are in the universe. Yet, tumbling Toast does not seem to care. If you drop your Toast while visiting Mars, whether it lands Buttered Side Down is determined by the size and position of the dropped Toast, according to Equation 5.4, and not on the value of g on Mars! Of course, it will fall more slowly on Mars, (because of smaller g) so you’ll have extra time to try to catch it. However, left to its own devices, the Toast will go through the same number of rotations as it falls off a Table on Mars as it will on Earth.

We have discovered something fundamental about the universe! Within the approximations I have made over my last few posts, Toast (or any rigid body) will fall and tumble based on its height, h₀, distance over the edge, d, and mass distribution, m / I, without regard for the value of the acceleration constant, g.

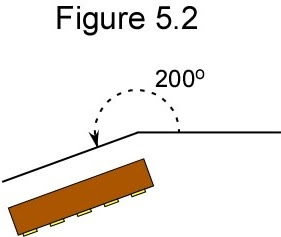
Ultimately, what does Equation 5.4 actually predict for the number of rotations? Using typical values for height h₀ = 0.75 meters (about 2.5 feet) and overhang d = 1 mm (0.04 inches). The moment of inertia for a 40 g piece of Toast that is shaped like a square with a length, l = 10 cm, and negligible thickness is I = m l² / 12 = 3.3×10^-5 kg m². Via Equation 5.4, we find θ is 3.0 radians or 200°.

This angle is only a little above the perfect Buttered Side Down condition at 180°. The small difference is illustrated in Figure 5.2. The Toast position in this illustration reveals that impact with the Floor will result in a Buttered Carpet.

(A simple approximation for the Landing Toast is that θ values between 90° and 270° result in the Buttered Side facing Down.)

Of course, the calculated result depends quite a bit on these chosen conditions. For instance, I just mentioned that Equation 5.4 is valid on any planet, but who is to say that aliens have the same size bread as we do? Since we don't know what Alien Bread is like, I'll compare across cultures on Earth, where a 10 cm piece of square Toast could be replaced with a 15 cm round object with the same mass, representing a tortilla (in Latin America) or pita (in the Middle East). Do Toasted Pitas suffer the same Buttered Side Down fate as Toast, or is Western European culture to blame for Greased Kitchen Floors? The moment of inertia of a thin, 40 g, 15 cm diameter circular Toast-Like Object is 5.63x10^-5 kg m². With the same initial conditions as used for the Square Toast, θ = 174°, also landing squarely Buttered Side Down.

Of course, the exact starting conditions chosen above seem a bit arbitrary. If I had used d = 4 mm or h₀ = 3 m, the Toast would have rotated twice as far and landed Buttered Side Up. 3 m is about 10 feet, considerably higher than most people position their breakfast, so we can ignore this case. However, the exact distance that the Toast overhangs the Table IS likely to vary quite a bit. Who is to say I will miss the Table by 1 mm? Perhaps I am clumsy enough to miss by 10 mm, resulting in more than 3 times as much rotation as I predicted above.

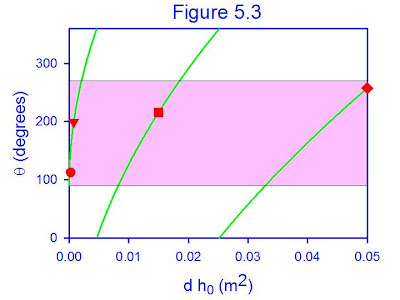This trend is presented graphically in Figure 5.3. In this figure, I've plotted Equation 5.4a with the values of m and I that I determined above, but leaving the product of d and h₀ as the independent coordinate. (the x-axis) (Here, the rotation angle increases with the square root of d h₀, starting from θ₀ = 90°. The y-axis wraps around at 360°, which is one full rotation, bringing the Toast back to the perfect Buttered Side Up condition, which is also θ = 0°.)

Several calculated points are marked in Figure 5.3. The circle corresponds to a gentle tumble off a Coffee Table, d = 1 mm and h₀ = 30 cm. The triangle is the calculation worked above, with d = 1 mm and h₀ = 75 cm. The square data point corresponds to an exceptionally clumsy person who drops the Toast while standing, so d = 10 mm and h₀ = 1.5 m, and the diamond is an extreme of this using d = 25 mm (out of a maximum of missing the table at d = 50 mm!) and h₀ = 200 cm (6.5 feet above the Floor!). The Buttered Side Down region has been shaded pink, revealing that there are many initial conditions that lubricate your carpet. However, as d h₀ increases, there are competing regions which do not.

Clearly, for small overhang (d) and low drop height, the non-slipping model predicts a Buttered Side Down landing. The universe really does hate you, and your Toast will land in the messiest possible position when it falls from a low position and only slightly unbalanced.

It is easy to seek limiting conditions where this prediction breaks down. For instance very Small Toast (such as a Buttered Cracker or Dipped Chip) will spin more easily, and a “low” falling height will be correspondingly lower. Thus, the scaling of Figure 5.3’s x-axis is much smaller and the Small Toast is likely to go through many rotations as it falls from a human-sized height. Since there are so many rotations on the way down, the number it goes through will be very sensitive to the exact h₀, and the result will appear to be “random.” In the other extreme, Large Toast (perhaps a Rigid Pizza) will not really fall or topple as described. In the extreme case, the Large Toast has such a large length that l/2 > h₀ and the Floor stops its fall before it even finishes toppling from the Ledge!

These trends will hold, even as I relax the approximations inherent to the non-slipping model. Thus, the propensity for Toast to land Buttered Side Down is entirely determined by the ratio of the size of our Toast to the height from which we drop it. That is to say, it depends on the size of our food relative to ourselves. More modest morsels (Small Toast) result in random landings, and Very Large Toast does more of a tip than a tumble from the Table.

Is there another factor, not included here, which cancels out the amount of overhang? My biggest simplification has been neglecting sliding. If the Toast were allowed to slide, the effective overhang, d, would be changing as it fell, and this might compensate for the exact starting conditions.

This is a postulated answer I will try to address (experimentally!) next time.

4. Toast in Free Fall

After the Toast leaves the Table Edge, its motion becomes particularly easy to describe. The reason for this simplicity is that gravity is the only significant force acting on the Toast. It falls according to the predictions of an object under uniform acceleration. (Uniform acceleration should be familiar to anyone who has taken an introductory physics class in high school or college. If not, a simplified treatment can be found here.)

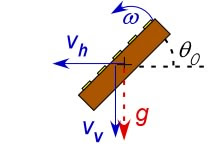
Unobstructed Toast soars through the air, requiring only a few parameters to describe its motion, as illustrated in the Figure. We start our stopwatch (t=0) when the Toast leaves the Table, noticing that the Toast may already be moving at this time. Based on my earlier discussion, any initial velocity was likely gained while tumbling off the table edge. It is useful to separate the velocity into two components: the vertical velocity v_v, which is parallel the gravitational acceleration (g), and horizontal velocity v_h.

The only thing v_h determines is WHERE the Toast lands. Unless you drop your Toast while brunching on the side of a very steep hill, this does not influence the height or time of the fall, so it does not impact the Buttered Side Down condition. Thus, assuming you are not a mountain goat, ignore v_h and just note that the Toast might land a few centimeters over from the Table Edge.

The other significant parameters are 1) the height (h₀) above the Floor at t=0, 2) the uniform gravitational acceleration (g=9.8 m/s² at Earth’s surface), 3) the angle of the Toast at t=0, θ₀ (the angle it rotated through before leaving the Table) and 4) its rotation rate, ω. (Rotational speed is also known as angular velocity, which can be a bit tricky to think about if you haven't before. It helps to think of angular speed similar to how you think of regular speed. Instead of miles per hour or centimeters per second, it measures flips per second or angle per second.)

Now let’s find the equations that describe what happens. (If you are not used to interpreting equations, be sure to read the comments in blue!) The height of the Toast above the Floor as a function of time is

(4.1) h(t) = h₀ - v_v t - ¹/₂ g t².

(Notice that at t=0, h(t) = h₀, which we expected from the definition of h₀. The second term, v_v t, is just velocity times time. The last term takes care of the extra speed the toast gains as it falls and is accelerated by gravity, as discussed here. )

The Toast hits the Floor when h(t)=0. By setting the right hand side of Equation 4.1 to 0 and solving for t, we find the time of the fall (t_f),

(4.2) t_f = -[ v_v - √ (v_v² + 2 h₀ g) ] / g.

(This can be found using the quadratic formula and verified by substituting back into Equation 4.1. Of course, quadratic equations have two solutions, but the second solution produces a time from before the Toast fell off the Table (t<0). Clearly, Equation 4.1 was not valid before the Toast fell because the Table was supporting the Toast! Therefore, we throw this other mathematical solution away because it does not represent our physical situation.)

Equation 4.2 is exact but overly complicated because the initial velocity is very small. (The fact that v_v starts off small was justified here, by assuming you have not hurled your toast energetically. I will also prove later that the amount it increases as the toast slides off the table is also quite small.) Neglecting v_v (i.e., setting it to zero) in Equation 4.1 and solving for t_f results in the much simpler expression

(4.3) t_f = √ ( 2 h₀ / g),

which we are much more likely to use later on. (When you drop an object, its time of flight only increases with the square root of distance because the longer it falls, the faster it goes at the end of the fall.)

Now that we know how long it takes for the Toast to fall, it is an easy matter to calculate how much it flips. The total flipping angle θ is

(4.4) θ(t) = θ₀ + ω t.

(Notice again that at t=0, θ(0) = θ₀, as we designed. Also notice the way θ(t) increases linearly with t, at a “speed” of ω. This will really drive home the physical meaning of ω!)

Equations 4.2 through 4.4 are the main results of this discussion, and we’ll refer back to them in later posts to predict the Buttered Side Down condition after approximating the Tumble from the Table.

3. How Toast Tumbles

Before proceeding down the slippery slope of calculations, we should consider the simple forces behind Buttered Toast Ballistics. Here, we’ll list the forces that act on the Toast and get a physical feel for why Toast Tumbles (flips end-over-end) when dropped.


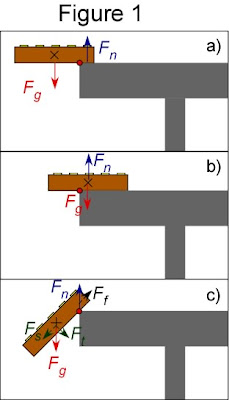
Figure 1a depicts the situation described previously as The Initial Conditions. To be explicit these are The Initial Conditions: The Toast starts on the Table Ledge, or some other surface about the same height, but we'll restrict that height to be between the surface of a low Table and the mouth of a tall person, standing. It is reasonable to assume most Toast spends most of its life between such altitude extremes. The Toast starts off with no velocity, thus we assume it has be placed clumsily, but not violently, in such a way it will topple and fall primarily under the influence of Gravity. The preferred orientation most people handle their toast is also Butter Up.

First, let's consider why Toast falls. This is easily understood by considering its placement on the ledge of the Table, with its center of mass beyond the ledge, as marked by the x in Figure 1a. Only two forces are relevant. Gravity is pulling down on the Toast (F_g, blue arrow) and the Table responds with the normal force (F_n, blue arrow). If the center of mass does not extend over the ledge (Figure 1b) then the Table supports the Toast, and the Toast does not move. Physically, the rigidity of the Table provides F_n equal and opposite F_g. More colloquially we’d say you successfully placed your Toast on the Table!


Many people find it intuitive that the Toast will rotate if the Table does not support its center of mass, as in Figure 1a. To see this explicitly, consider the red dots in Figure 1. These dots mark the Table Ledge, the axis around which the Toast will rotate. In Figure 1b, more of the Toast’s mass lies on the right of the red dot than the left, so it would try to rotate clockwise. However, the Table supports the right hand side, so the Toast just sits there. In Figure 1a more of the Toast is on the left of the red dot, so the Toast tries to rotate counterclockwise. There is nothing to support the left side of the Toast and we soon end up in the situation in Figure 1c, with the Toast rotating and angled as it tumbles off the Table.


The same two forces are still present, gravity and the Table’s rigidity. The situation in Figure 1c is more complicated because more things are happening. Focusing on gravity, we notice that it does two things to the Angled Toast. Even as the Toast rotates, F_g helps it rotate faster by pulling at a right angle to the line connecting Toast’s center of mass to the pivot point at the Table Ledge. (This is caused by the torque τ = F_g x d. People who have studied physics previously will recognize that it is now necessary to consider the vector nature of forces to quantify what is going on.) For this discussion, we notice that only a component of F_g torques the Toast and makes it spin faster, so we label this portion F_t. The other component of F_g is pulling along the length Toast, causing it to slide off the Table, so we label it F_s. Once the Toast begins to tilt, we distinguish these two components of gravity (the green arrows in Figure 1c) according to what type of motion they produce: making the Toast tilt faster (F_t), and causing sliding off the Table (F_s). (Notice that these are not new forces, but a new way to describe the forces present, based on the type of motion they produce. Gravity always pulls the Toast straight down. What is changing is the geometry of the Toast-Table system, so gravity’s tug moves the Toast in a slightly different way.)


The Table Ledge also behaves a bit differently. F_n is still present, but we now must add a force of friction, F_f, which opposes the sliding of the Toast. The black arrow in Figure 1c represents this force, which was not relevant in Figure 1a and 1b until we began considering sliding and pondered the force that opposed it.


All these forces act in concert; by the time the Toast leaves the Table, there will be several types of motion. Most importantly for the Buttered Side Down discussion, the Toast will be tumbling end over end. However, the sliding will likely cause some lateral motion (to the left), and it will already be falling toward the floor when it leaves the Table. Importantly, once the Toast leaves the Table it will be in free fall; it will accelerate vertically, but its tumbling and lateral motions will be constant without the influence of the Table. Thus, whatever conditions we calculate for the Toast as it leaves the Table will be easily extended to the time at which it hits the floor. All the hard work will be performed in calculating what is going on with the Toast before it leaves the Table.


A purist might say that Toast will experience drag (friction from the air) as it falls, which will change its lateral and tumbling motion. Although I will directly confront this at some point down the road, drag forces should be fairly negligible at the typical speeds that Toast moves. There are several other forces present that I have not mentioned yet, including the Coriolis effect in Earth’s rotating reference frame, and tidal forces from the moon and sun. Clearly, not all of these are important. Instead of trying to include EVERYTHING at once, it is better to come up with a simple model and then add complications and see which ones are important and what is needed to make theory and experiment agree. In fact, we’ll start even simpler, without including all of the effects included in this discussion, as it is useful to see what happens in the absence of sliding.

2. Mathematics May Follow!

I have two opposing goals with this blog. 1) I want it to be accessible to the casual reader. 2) I intend for it to still be scientifically accurate, which means I must include the equations and numbers that make the science useful and clear.

Here, are some conventions I'll use to try to satisfy these inherently conflicting goals.

First, post numbers correspond to the order in which I publish related posts on the same topic. This is also the order they should be read if you’re interested in reading the whole blog. Or not, but you may find yourself looking back at links to previous posts as I use the results from them.

Capital Letters will be used to emphasize some of the main objects discussed in this blog, including Toast, Ledges, Tables, Floors, Butter, and, of course, the Buttered Side Down Condition. Think of these as proper nouns, the names of our friends in this journey, which are capitalized like any other proper noun, like Mrs. Bush, Scranton, PA, or Chuck Norris.

Allegedly, equations and math generally scare away readers who aren't used to dealing with them. To amend this, I intend to insert detailed discussion of the math and science points as necessary, as might be found in a popular book about physics where equations might be omitted entirely. However, I will include such discussion in parenthesis (and colored blue, like this) so this extra information can be skipped by anyone who already understands what's going on and doesn't want to deal with the extraneous recap of familiar science or math. I’ll use other colors as I see fit, such as red to draw attention to certain sections.

That said, I've also found that getting mathematical equations into Blogger isn't all that easy.

Luckily, I found 2below0's list of code for HTML4 Greek symbols, and a link to more general HTML4 character escape sequences. So I can finally express the irrational number 3.14159... (represented as π) as it's symbol, and I don't have to spell out "pi". Hopefully all my readers will have HTML4 compatible browsers or otherwise be able to interpret the escape sequences.

Despite offending many people's delicate sensibilities, I'm going to stick with whatever font this is by default, because it makes the letters I and l distinguishable (versus the subtle I and l in Arial, for instance).

For expressions involving complicated numerator and denominators, I'm going to leave everything in parenthesis and separate the two with a widely spaced "/" symbol, so x/y will become

(x) / (y)

and more complicated ratios will be understandable as well.

Similar parenthesis-based notation will be used with square roots, so hopefully it will be obvious that

√(x)

is the square root of x.

I'll probably append this post with more conventions as they are created.

1. Does Toast Always Land Buttered Side Down?

That is the question to be addressed in this blog. My posts will be a series of "lab book" entries as I explore the Buttered Side Down Phenomenon. By the time I finish, I hope to have addressed a variety of topics regarding Tumbling Toast, and maybe even generate publication-worthy results addressing humankind's age-old question about how breakfast is ruined.

Some people dismiss the Buttered Side Down Phenomenon as pessimism or the selective generation of memories following a Ruined Breakfast. Others have suggested otherwise, and attempted to prove it. These vary from the facetious study mentioned here, to the serious attempt by Matthews that inspired my interest in the Buttered Side Down Phenomenon. More recently, the BBC's H2G2 published an accurate, if opaque, explanation. In this study I intend to bridge the gap between Matthews' rigor and H2G2's web-based discussion.

A study "busting" the Buttery Landing Hypothesis was published by the quasi-experimental geniuses (experimental quasi-geniuses?) at Mythbusters, who catapulted toast through the air and found that it landed on the Buttery Side randomly, i.e. approximately half of the time. Yet, they admitted that when toast topples from a table it does tend to land upside down. Thus the subtleties of H2G2's and Matthews' arguments became yet another victim to the spectacle that is television, which unjustly focused on the unusual phenomenon of Violently Hurled Toast.

There is nothing magical about toast that draws The Buttery Side to the ground, but it does fall in a very particular way. Most people hold their toast or put it on the table Buttered Side Up. Also, with some notable cinematic exceptions, breakfast tends to be a low-energy environment, tending not to produce High Kinetic Energy Bread. Thus, Tumbling Toast most likely falls gently from about tabletop or mouth height, generally starting with the Buttery Side up. These observations are what physicists call the Initial Conditions, the starting point for theoretical predictions and the way experimental studies are prepared. In the posts that follow, I will begin exploring the consequences of The Initial Conditions.